Most elegent design I’ve ever seen…
Mundane Turing Machine
A machine in every move, read a symbol from the current position of its head on a tape, from its state register and the symbol read to find the next instruction from its table, then based on the instruction, write a symbol with head, update its state register, and chooses to move left/right or halt.
Reference: See wikipedia.
Question:
Wouldn’t turing machine in N-Dimentional Space to be interesting…the head could move in an arbitary direction…
Overall Archtecture
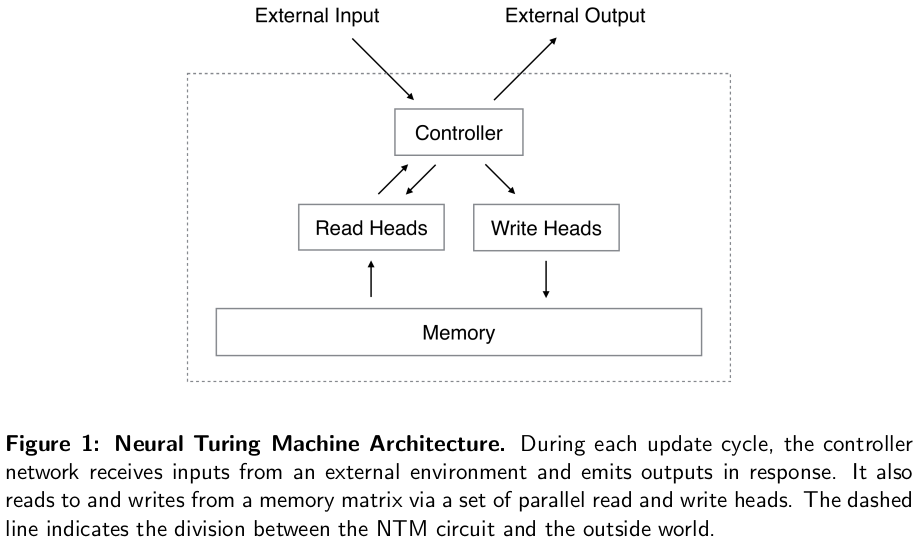
Difference:
A neural network is used to replace the mundane table, just like what the Deep Q-learning did. So this is basically a Q-learning model with a differertiable memory bank!
Memory Operations
In compensation to that, the memory need to be be differentiable to update by gradient descent.
Define memory to be a $M\times N$ Matrix $M_t$. It is seemed as a memory with $N$ entries, and each entry have a capacity of $M$.
Read Operation:
The read head emits a softmaxed vector $w_t$ of length $N$, the read $1 \times M$ vector $r_t$ would be
$$r_t=\sum_i^N{w_t(i) \times M_t(i)}$$
very intuitive.
Write Operation:
Write head emits a softmaxed weighting vector $w_t$ to specify which entries of matrix will be modified.
For erase, the write head emits a softmaxed erase vector $e_t$, and erase contents by the two weightings:
$$\dot M_{t+1}(i) = M_t(i)*(1-w_t(i)e_t(i))$$
For writing, the write head emmits a addition vector $a_t$ to add to the selected contents:
$$M_{t+1}(i)=\dot M_t(i) + w_t(i)a_t(i)$$
Addressing
The afore-mentioned weighting vectors are used to operate selected entries, but to select the entries in a diffenertiable way, we need two addressing mechanisms, namely: Content-based Addressing and Location-based Addressing.
Overall Addressing Diagram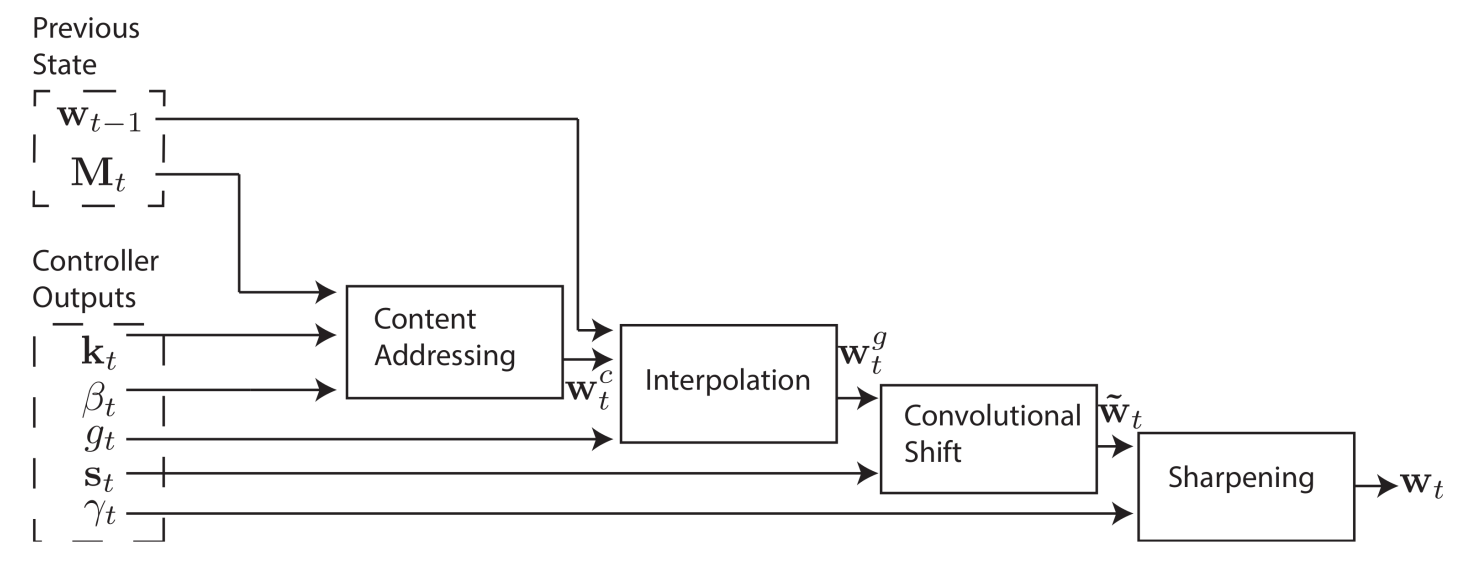
Content-based Addressing
It allows the network to select entries by stating its content, so that it could update it. The head emmits a vector $k_t$ length of $M$, which is compared to each entries to get a content similarity vector $w^c_t$ of length $N$
$$w^c_t(i) = \frac{k_t \cdot M(:,i)}{||k_t||\cdot||M(:,i)||} $$
. This weighting is then normalized by softmax to further attenuate smaller values and amplify larger values.
Location-based Addressing
It allows the network to get the memory of a location without knowing what’s inside.
First, each head need to provide a scalar interpolation gate $g_t$ to specify which type of addressing is to be used in order to get the current memory:
$$w^g_t = g_t w^c_t + (1-g_t) w_{t-1}$$
In terms of location-based addressing, there are three possible actions, namely to shift: $-1,0,1$ entry to the right, same as a mundane turing machine. This is controlled by a length $3$ softmaxed vector $s_t$ provided by the head. other than softmax, using a shift scalar emitted by the controller as lower bound to simply clip the outputs is also experimented.
In order to perform the selected shift, a circular convolution is performed on memory $M_t$ by performing that on its index, namely, $w^g_t$, basically rolling the weighting vector $w^g_t$ by $s_t$.
$$\dot w_t = \sum_{j=0}^{N-1}w^g_t(j)s_t(i-j)$$
Sharpening
Inevitably the rolled weighting vector $w_t^g$ will be blurry due to the diffenertiable nature of the roll. A sharpening operation using a scalar $\mathcal{Y}_t \geqslant 1$ emmitted by the head.
$$w_t(i) = \frac{\dot{w_t}(i)^{\mathcal{Y}_t}}{
\sum{\dot{w_t}(i)^{\mathcal{Y}_t}}
}$$
Controller Network
Both feed-forward neural network and LSTM are considered to be used as controller. However, due to the fact that currently only one reading/writing head is used, simple operations like multiplying two numbers in memory is made impossible for a feed-forward network. Thus those units of recurrent nature would works better.
Reference
Neural Turing Machines 2014. Alex Graves, Greg Wayne & Ivo Danihelka