Method:
For every layer’s output in a densely connected net, calculate its mutual information with the input $X$ and output $Y$.
Plot the two mutual information of each layer against each other. Observe change as the model is being trained.
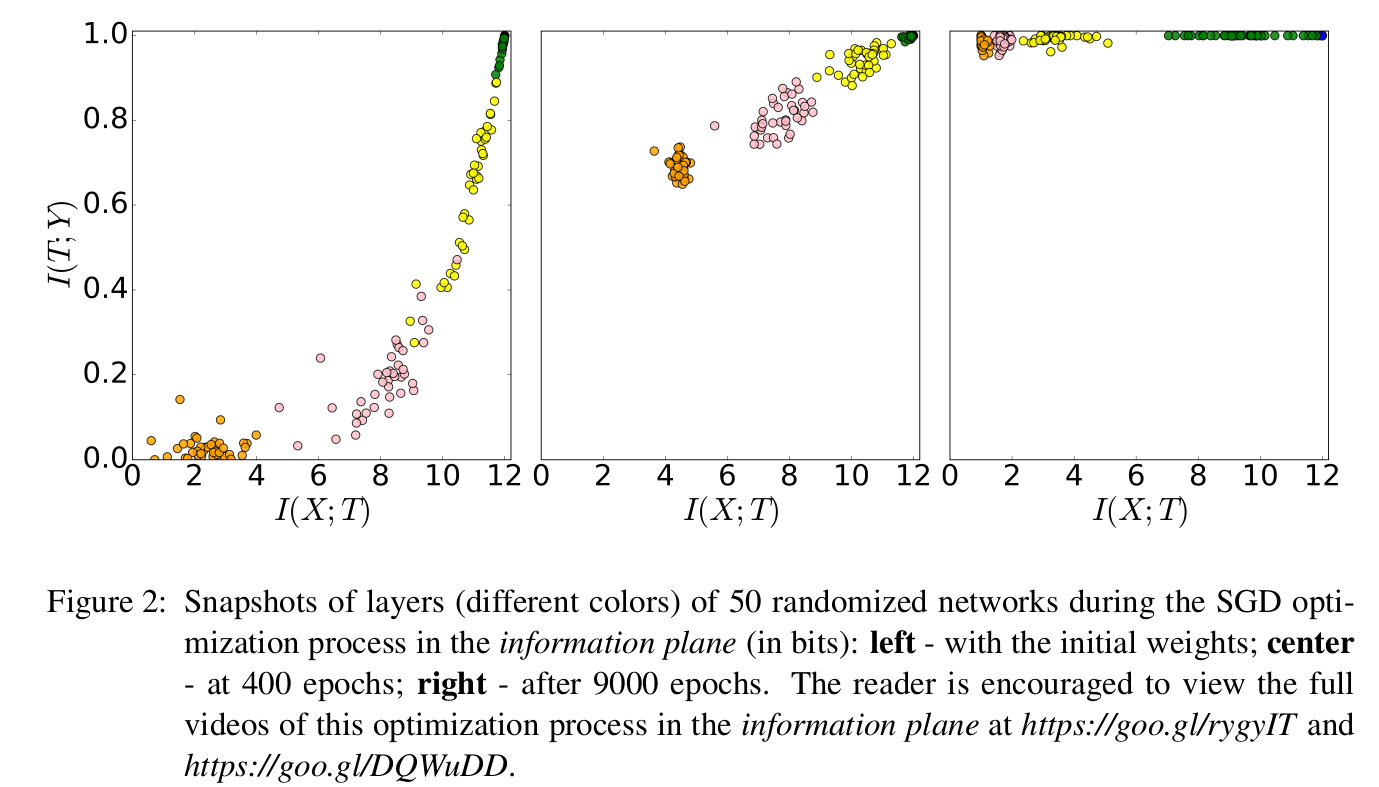
NOTE: This network have exactly 12 bits of input and 2 bits of output.
Before training:
As a matter of fact, we observe the input layer(green) tells everything about the input itself, and almost everything about the output itself. Since all weights are randomly initialized, as the network goes deeper (further left bottom to the graph), less mutual information are contained against both $X$ and $Y$.
After training:
The layer outputs contains less information about the input, but more about the output.
What is important: The Middle: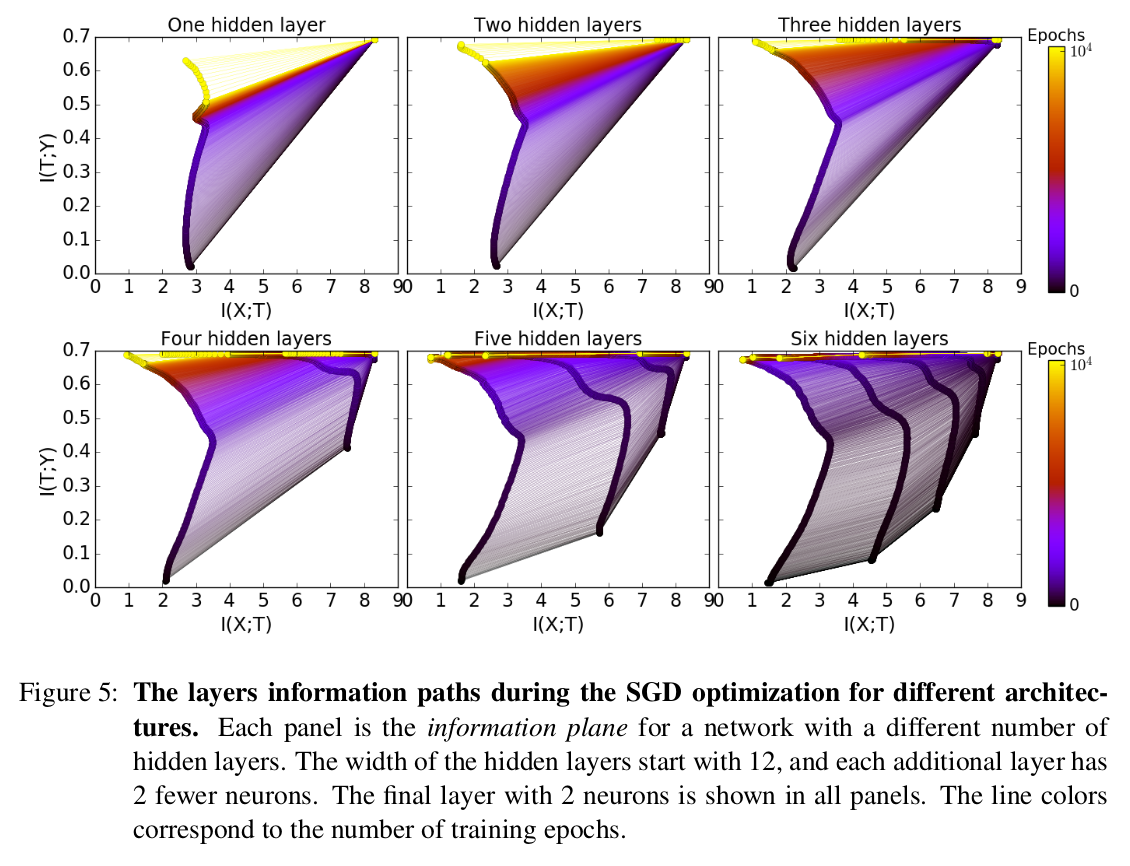
Looking at a graph of how each layer moves along the training process, two distinct phases could be found, where in the first phase the layer contains more information of $Y$, where training error decreases. This phase happens fast. The second phase, taking most of the epoches, is a process of eliminating information of $X$ from the layer output. It is viewed as the process of generalization.