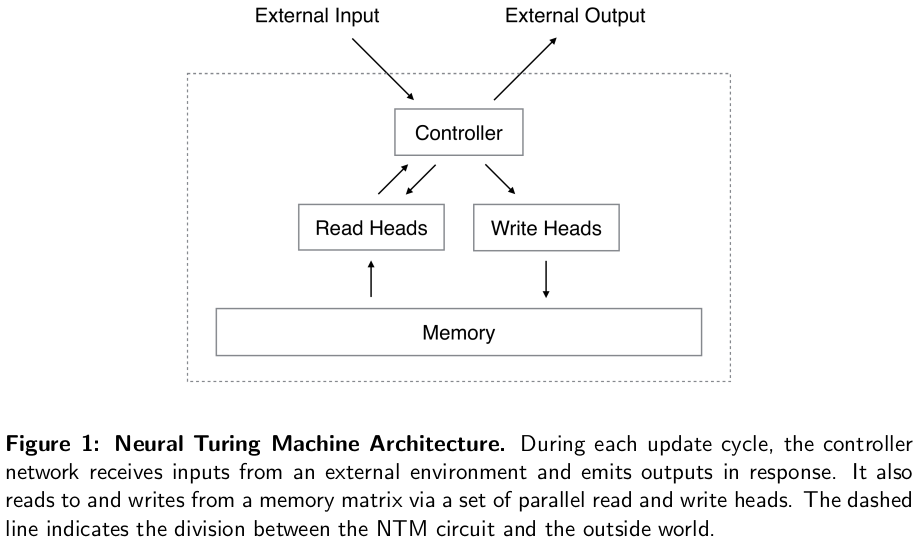
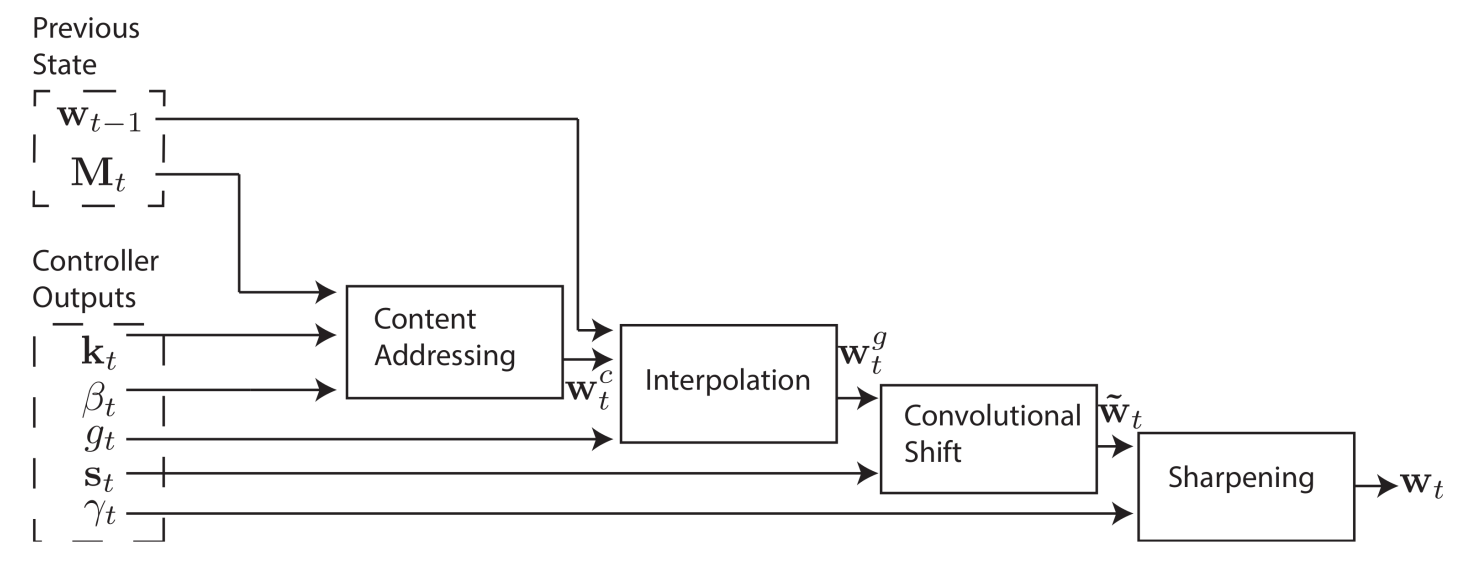
Spoilers Alert: Reading this will kill all your fun figuring out how to register at Hack The Box . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

–

Now Let’s Begin!

From this page we start.

1 . Looking into the source of the pages, we shall find a script called /js/inviteapi.min.js. Open it just to realize it is a piece of code decoding itself into actual codes.

We can beautify it and read it:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

eval(
    function(p,a,c,k,e,d){
        e=function(c){return c.toString(36)};
        if(!''.replace(/^/,String)){
            while(c--){
                d[c.toString(a)]=k[c]||c.toString(a)
            }
            k=[function(e){return d[e]}];
            e=function(){return'\\w+'};
            c=1
        };
        while(c--){
            if(k[c]){
                p=p.replace(new RegExp('\\b'+e(c)+'\\b','g'),k[c])
            }
        }
        return p
    }
    ('1 i(4){h 8={"4":4};$.9({a:"7",5:"6",g:8,b:\'/d/e/n\',c:1(0){3.2(0)},f:1(0){3.2(0)}})}1 j(){$.9({a:"7",5:"6",b:\'/d/e/k/l/m\',c:1(0){3.2(0)},f:1(0){3.2(0)}})}',
        24,
        24,
        'response|function|log|console|code|dataType|json|POST|formData|ajax|type|url|success|api|invite|error|data|var|verifyInviteCode|makeInviteCode|how|to|generate|verify'.split('|'),
        0,
        {}
    )
)

2 . But there isn’t much point to really figure out how everything is decoded, because we can just run it inside the console with some slight modifications:

1
2

// Running this in the console
function testt(p,a,c,k,e,d){e=function(c){return c.toString(36)};if(!''.replace(/^/,String)){while(c--){d[c.toString(a)]=k[c]||c.toString(a)}k=[function(e){return d[e]}];e=function(){return'\\w+'};c=1};while(c--){if(k[c]){p=p.replace(new RegExp('\\b'+e(c)+'\\b','g'),k[c])}}return p};testt('1 i(4){h 8={"4":4};$.9({a:"7",5:"6",g:8,b:\'/d/e/n\',c:1(0){3.2(0)},f:1(0){3.2(0)}})}1 j(){$.9({a:"7",5:"6",b:\'/d/e/k/l/m\',c:1(0){3.2(0)},f:1(0){3.2(0)}})}',24,24,'response|function|log|console|code|dataType|json|POST|formData|ajax|type|url|success|api|invite|error|data|var|verifyInviteCode|makeInviteCode|how|to|generate|verify'.split('|'),0,{})

returns what we want(beautified)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

function verifyInviteCode(code){
    var formData={"code":code};
    $.ajax({type:"POST",
        dataType:"json",
        data:formData,
        url:'/api/invite/verify',
        success:function(response){console.log(response)},
        error:function(response){console.log(response)}})
}
function makeInviteCode(){
    $.ajax({type:"POST",
        dataType:"json",
        url:'/api/invite/how/to/generate',
        success:function(response){
            console.log(response)
        },
        error:function(response){
            console.log(response)
        }})
}

3 . What we are interested will be the makeInviteCode(). Run it and we got a reply of Va beqre gb trarengr gur vaivgr pbqr, znxr n CBFG erdhrfg gb /ncv/vaivgr/trarengr:

4 . Find some ROT13 decoder and decode it, we get In order to generate the invite code, make a POST request to /api/invite/generate.

5 . That seems clear enough, that all we need is to replace /api/invite/how/to/generate to /api/invite/generate and run everything again in the console like this:

1
2
3
4
5
6
7
8
9
10
11
12

function makeInviteCode(){
    $.ajax({type:"POST",
        dataType:"json",
        url:'/api/invite/generate', // Change here
        success:function(response){
            console.log(response)
        },
        error:function(response){
            console.log(response)
        }})
}
makeInviteCode();

6 . This time we received a base64 encoded string S0NMWVctWEJFV0QtVE1QSkwtVkxFVVAtV0xXTkE= (might differ for different trials).

7 . Decode it and we have our invitation code!

1
2

~$ echo "S0NMWVctWEJFV0QtVE1QSkwtVkxFVVAtV0xXTkE="|base64 -d
KCLYW-XBEWD-TMPJL-VLEUP-WLWNA

8 . Enter the code and start the adventure!

Use Redstone if you are color blind.

EVERY SINGLE SEASON!!!

Fan arts inspired by the XKCD comics.

For 5-dimensional users, please use Quaternions instead.

Fan arts inspired by the XKCD comics.

Apparently the current version of WPILib(1st 2019 official release) isn’t happy with our ADXRS450 Gyros, and the getAngle() call always return zero.

Sadly the workaround, although present, doesn’t seems to be indexed by google yet…which is why I am making this post so more people could see it before deciding to spend their precious budget buying a new one, like us.

The workaround is found here, which I will present a copy here:

Auto SPI Does not work in v12 image (affects Analog Devices IMUs and Gyro))

The Auto SPI functionality used by Analog Devices IMUs (ADIS16448 and ADIS16470) and Gyro (ADXRS450) does not work correctly in the 2019-v12 image that is part of the kickoff release.

Workaround: After imaging, log into the robot console as admin (via serial or SSH) and run the command “updateNIDrivers”, then reboot. A simplified tool to execute this is in progress and more information about a full update with this issue resolved will be coming soon.

Solution: We will be issuing an updated FRC Update Suite with a new image that resolves this issue.

Anyway… If u are still unsure what to do:

1. Connect to Roborio-connected router
2. Open a terminal in an *nix/Macos/FreeBSD system, or use an emulator like Putty on Windows.
3. SSH to the Roborio using username admin and an empty password. By default configuration, the command is : ssh admin@10.71.46.2
4. Run updateNIDrivers, and reboot.
5. Since the workaround require rebuilding the kernel, which is quite resource hungry, you may want to kill the running robot code by mv /home/lvuser/robot_java.jar /home/lvuser/robot_java.jar.disable;killall /usr/local/frc/JRE/bin/java;updateNIDrivers.
6. Later mv /home/lvuser/robot_java.jar.disable /home/lvuser/robot_java.jar and reboot.

Especially suitable for high-school essay prompt generation.

Fan arts inspired by the XKCD comics.

Fan arts inspired by the XKCD comics.

Fan arts inspired by the XKCD comics.

Fan arts inspired by the XKCD comics.

Most elegent design I’ve ever seen…

Mundane Turing Machine

A machine in every move, read a symbol from the current position of its head on a tape, from its state register and the symbol read to find the next instruction from its table, then based on the instruction, write a symbol with head, update its state register, and chooses to move left/right or halt.

Reference: See wikipedia.

Question:
Wouldn’t turing machine in N-Dimentional Space to be interesting…the head could move in an arbitary direction…

Overall Archtecture

Difference:
A neural network is used to replace the mundane table, just like what the Deep Q-learning did. So this is basically a Q-learning model with a differertiable memory bank!

Memory Operations

In compensation to that, the memory need to be be differentiable to update by gradient descent.

Define memory to be a $M\times N$ Matrix $M_t$. It is seemed as a memory with $N$ entries, and each entry have a capacity of $M$.

Read Operation:
The read head emits a softmaxed vector $w_t$ of length $N$, the read $1 \times M$ vector $r_t$ would be
$$r_t=\sum_i^N{w_t(i) \times M_t(i)}$$
very intuitive.

Write Operation:
Write head emits a softmaxed weighting vector $w_t$ to specify which entries of matrix will be modified.

For erase, the write head emits a softmaxed erase vector $e_t$, and erase contents by the two weightings:
$$\dot M_{t+1}(i) = M_t(i)*(1-w_t(i)e_t(i))$$

For writing, the write head emmits a addition vector $a_t$ to add to the selected contents:
$$M_{t+1}(i)=\dot M_t(i) + w_t(i)a_t(i)$$

Addressing

The afore-mentioned weighting vectors are used to operate selected entries, but to select the entries in a diffenertiable way, we need two addressing mechanisms, namely: Content-based Addressing and Location-based Addressing.

Overall Addressing Diagram

Content-based Addressing

It allows the network to select entries by stating its content, so that it could update it. The head emmits a vector $k_t$ length of $M$, which is compared to each entries to get a content similarity vector $w^c_t$ of length $N$
$$w^c_t(i) = \frac{k_t \cdot M(:,i)}{||k_t||\cdot||M(:,i)||} $$
. This weighting is then normalized by softmax to further attenuate smaller values and amplify larger values.

Location-based Addressing

It allows the network to get the memory of a location without knowing what’s inside.

First, each head need to provide a scalar interpolation gate $g_t$ to specify which type of addressing is to be used in order to get the current memory:
$$w^g_t = g_t w^c_t + (1-g_t) w_{t-1}$$

In terms of location-based addressing, there are three possible actions, namely to shift: $-1,0,1$ entry to the right, same as a mundane turing machine. This is controlled by a length $3$ softmaxed vector $s_t$ provided by the head. other than softmax, using a shift scalar emitted by the controller as lower bound to simply clip the outputs is also experimented.

In order to perform the selected shift, a circular convolution is performed on memory $M_t$ by performing that on its index, namely, $w^g_t$, basically rolling the weighting vector $w^g_t$ by $s_t$.
$$\dot w_t = \sum_{j=0}^{N-1}w^g_t(j)s_t(i-j)$$

Sharpening

Inevitably the rolled weighting vector $w_t^g$ will be blurry due to the diffenertiable nature of the roll. A sharpening operation using a scalar $\mathcal{Y}_t \geqslant 1$ emmitted by the head.
$$w_t(i) = \frac{\dot{w_t}(i)^{\mathcal{Y}_t}}{
\sum{\dot{w_t}(i)^{\mathcal{Y}_t}}
}$$

Controller Network

Both feed-forward neural network and LSTM are considered to be used as controller. However, due to the fact that currently only one reading/writing head is used, simple operations like multiplying two numbers in memory is made impossible for a feed-forward network. Thus those units of recurrent nature would works better.

Reference

Neural Turing Machines 2014. Alex Graves, Greg Wayne & Ivo Danihelka